教育を面白くするメディア 「エデュモット」東京学芸大学公式ウェブマガジン

vol.19 田中心先生

お待たせいたしました！edumotto版「せんせいのーと」第二弾は数学科の田中心先生です。結び目理論ってなんでしょう…？っえ、数学なの！？興味をもったそこのあなた！！この記事を読んで、一緒に結び目の魅力に迫っていきましょう！！

先生のご専門を教えてください

田中先生：数学の中でも、幾何学が専門です。わかりやすくいうと図形の分野ですね。幾何学は位相幾何学（いそうきかがく）と微分幾何学に分けられますが、私は位相幾何学を専門としています。

位相幾何の位相ってどういう意味ですか？

田中先生：あらためて聞かれるとむずかしいですね（笑）。位相というのは、「位置と形相」を省略したものといわれています。形相は「かたち」のことですね。たとえば、ボールをチョップすると表面がへこみますが、位相幾何学では、チョップの前も後もボールはボールなので、前後で本質的な「かたち」は変わらないと考えます。微分幾何学では、チョップの前後でボールの表面の曲がり方の様子が異なる点に注目します。

位相幾何学の考え方を説明する例としては、「コーヒーカップもドーナツも同じと考える」というのが有名です。ふたつはまったく違う形状に見えるけれど、コーヒーカップには持ち手の「穴」、ドーナツには真ん中に「穴」があり、どちらも「穴が一つ」という共通点を持っていますね。

切ったり貼ったりはできませんが伸縮は自在とし、仮想的にのばしたり縮めたりして移り合えば同じものと考えるんです。このように、本質的なつながり方に着目して図形の「かたち」を調べるのが位相幾何学です。

位相幾何学は社会の中でどう役立っているのですか？

田中先生：たとえば、「路線図」には位相幾何学の考え方が利用されています。山手線の路線図を思い浮かべたとき、実際の地図通りの形よりも円形を思い描く人は、多いのではないでしょうか。つながり方さえ分かればそれで十分で、より平易に表したほうが便利ですよね。こんな風に、私たちも位相幾何学を知らず知らずと使っているのです。私はその中でも、「結び目理論」 という分野を専門にしています。

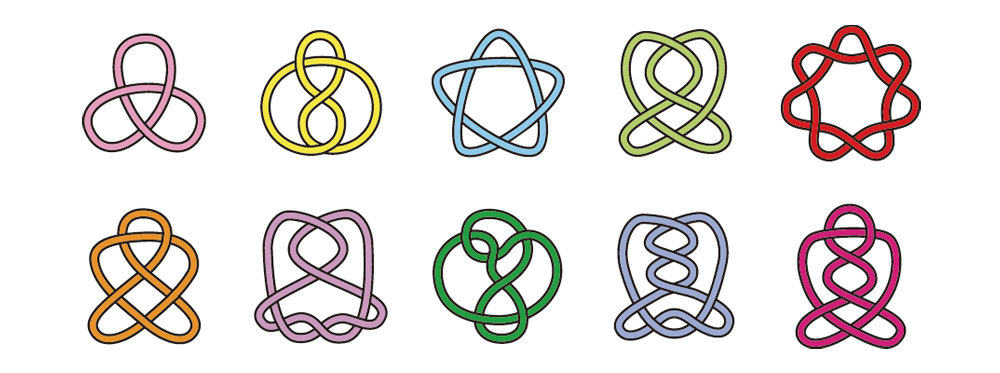
(イラスト提供：田中先生)

その「結び目理論」とはなんでしょうか？

田中先生：結び目というと靴ひもや、荷造りの紐などがありますが、どちらの結び目も端からスルスルとほどくことができますよね。荷造りの場合は固く結んでしまうので、スルスルとはいかないかもしれませんが（笑）。そこで、数学で結び目を研究するときは、両端を接着して閉じた状態にします。つまり、「空間内で結ばった輪っか」を扱うわけです。下にある二つの結び目は、明らかに違う結び目に見えますが、その違いを数学的に調べるのが「結び目理論」です。これら二つは絶対に同じにはならないのですが、「（同じに）ならなそうだから、ならない」では理由になりません。

たとえば、下の一番左の結び目は一見すると上の右側と同じに見えますが、徐々に変化させていくと上の左側の結び目と同じであることがわかります。このように見た目だけで判断するのは危険です。数学では「これこれしかじかという理由で、決して同じにはなりません」と、論理的に証明を与える必要があります。

(イラスト提供：田中先生)

どんなところに魅力がありますか？

田中先生：遊びの要素としては、2010年頃に考案された「領域選択ゲーム」があります。大阪市立大学の河内明夫名誉教授と、当時の研究室の方達が考案しました。
（参照：大阪市立大学数学研究所　領域選択ゲームのウェブサイト）

ひと筆書きで描いた閉じた曲線の交差点に、オンとオフになるランプがついていて、囲まれた領域を押すと、境界線上にあるランプのオンとオフが切り替わる。これを繰り返して、すべてのランプをオンにするゲームです。Androidのアプリにもなっています。このゲームのおもしろいところは、どんなパターンから開始しても必ず全部のランプをオンにできるところです。閉じた曲線をひと筆書きで好きに描いて、交差点のオンオフの情報を自分で自由に設定しても、絶対解けるようになっています。それが理論的に証明できるのです。そこに「結び目理論」が使われているんですよ。

おぉー！絶対解けるというのがすごいですね。遊び心をくすぐられます！
それでは、高校生にも読めるような、おすすめの本はありますか？

田中先生：このゲームをつくった先生方が書いた『結び目理論とゲーム』（河内明夫・岸本健吾・清水理佳 著／朝倉書店）という本があります。領域選択ゲームを通して結び目理論のおもしろさをわかりやすく解説しています。
ほかにおすすめなのは『ゲームで大学数学入門』（安田健彦 著／共立出版）という本です。ゲームを通して大学数学を解説しているユニークな本です。位相幾何学のアイデアが背景にあるゲームも扱われていて、著者自身が考案したオイラー・ゲッターというゲームが最後に紹介されています。高校までとは違った数学に触れることができるので、高校生でも興味を持てれば読めるのではないかと思いますね。

学校教育で結び目理論はどう生かせますか？

田中先生：空間図形を把握する力を高める教材として使えるのではないかと思っています。空間図形というと、今までに立方体や三角錐や球などを扱ってきたかと思いますが、実際に作って触れてみるとなると、正確に作るのは難しく、工作をするのに意外と時間がかかると思います。それと比べると「結び目」はひも状のもの（と両端を接着するもの）があれば比較的簡単に作れます。

たとえば、結び目をロープや延長コードなどで実際に作ってみて、それを紙に描きとらせるのはどうでしょうか。空間図形を平面に図示する経験を踏まえることで、教科書という平面に書かれた空間図形をより認識しやすくなるはずです。あるいは逆に、紙の上に描かれた結び目の絵を、実際に空間内の結び目をロープや延長コードで作ってみるのもよいと思います。さらに進んで、空間内で結び目の見た目を変えてみて、その変化する様子を紙に描いて説明するのもおもしろそうです。

こんな風に大学数学も数学教育に応用できると思うんです。「どうしてこうなるのか」を説明できるようになるのはもちろん大事だけれど、まずは体験してみて「楽しい！」と思えることが重要なんですよね。

先生が数学や幾何学に興味を持ったきっかけは何ですか？

田中先生：小中学校の算数・数学で、作図とか平面図形などが好きだったというのが、最初のきっかけだったのかな。大学の数学はそういうものとは全然イメージが違いますが、元をたどるとそこから数学をやろうと、幾何学を選んだのだと思います。

小学校のころから算数・数学ひと筋だったのですか？

田中先生：子どものころから、算数・数学好きの少年でした。小学校のときの塾の先生がとてもおもしろい先生で、印象に残っています。学校の授業では扱わないような、難しい発展的な問題に触れてくれたんですよ。それがすごくおもしろかったですね。
それと、音楽は好きで、小学校のころ、エレクトーンやピアノを習っていました。でも高学年の時にやめてしまいました。今となっては、続けていればよかったなあって思います。音階は数学的だから、通じる部分があるのかもしれないですね。

学生時代はどんな学生でしたか？

田中先生：それなりに真面目な学生でした。友人数名と輪講形式で勉強したりしていました。数学の専門書を参加者全員で分担し、各人が順に発表者となって分担内容を講義する、いわゆるセミナー形式の勉強会です。アルバイトは家庭教師や塾講師をやっていました。数学以外は担当したことがないですね。
4年生で微分幾何学の研究室に入りました。数学のゼミは、先生の指導を受けながら輪講する形で行われます。数学の学習方法としては「究極のアクティブラーニング」だと思っています。ゼミ生は6人で、そのうち3人が3年生でした。飛び級で所属している、ものすごくできる人たちがいて、そこで少し挫折感を味わいましたね。そのまま同じ大学の大学院に進むつもりだったけれど、別の大学の大学院にも運よく受かったので、環境を変えようと外に出ました。大学院では位相幾何学の研究室に入って、先生に勧められて、結び目理論と出会いました。

それまであまり社交的ではなかったのですが、「ここで心機一転しよう」と思いました。積極的に交流するようになったおかげで、他大学の院生の友人ができたりしました。トポロジー（位相幾何学）の分野でも全国の院生が集まる合宿形式のセミナーがあって、みんなで山に登ったり、夜はお酒を飲んだりして、いろいろな知り合いができてどんどんおもしろくなりました。そういうなかで切磋琢磨していきましたね。

いまでも数学ひと筋の人生ですか？

田中先生：いや、いまは3歳の子どもがいるので、子どもが趣味みたいになっていて（笑）。最近は子どもがすごろくにハマっていて、よく一緒にやっています。飽きるまでエンドレスなのが少し大変ですが、日々成長が感じられて楽しいです。先日は七五三だったので、たくさん写真を撮ったりしました。

これからの目標を教えてください。

田中先生：実は、位相幾何学が（私自身が？）ここ数年、学内で人気がないんです。過去にはすごく人気のある年もあったのですが、オンライン授業などの影響もあるのかもしれません。大学で学ぶ数学にもっと興味をもってもらいたいと思っています。

学芸大生は「先生になるために数学教育を学びたい」と考えている人が多く、数学自体に興味を持って授業を受ける人が少ない気がします。私を含め教員側が数学の魅力を伝えきれていないのかもしれません。中高の数学よりももっとその先の数学も探求してほしいと思っています。10を教えるためには20、30を知っておく必要があるはずだから。

ただ、大学数学の授業を学生による探求型のような形で展開するのは現実的ではないため、どうしても一方的に教える授業展開になってしまうのは仕方ないのかなと思っています。なかなか難しいですね。

中高生で、数学に興味のある子たちに伝えたいことはありますか？

田中先生：受験にとらわれずに、「考え抜く」という経験をするといいかな。解けなくてもいいから、考えることが大事だと思うんです。やり方を覚えて繰り返す勉強、そこから一歩離れて、自由に数学と向き合ってほしいです。

レゴブロックを組み上げていろんなものを作るのって楽しいですよね。数学にもそういう楽しさがあると思っています。研究に入る前の勉強段階では「人の作った作品をまねて作る」楽しさが、研究段階では「自分で好きに組み上げて作品を作る」楽しさがあります。なんなら、自分で新しい形のブロックを考案し、組み上げてもいいんです。ちょっとした簡単なことでいいから、自分で数学を作り出す経験ができるといいですね。

田中 心

自然科学系数学講座　数学分野　准教授

1979年生まれ、岡山県出身。小学校高学年のころから徐々に「算数・数学」の楽しさにハマっていく。愛光高校、京都大学理学部、東京大学大学院数理科学研究科で学び、2006年3月に博士（数理科学）を取得。日本学術振興会特別研究員、学習院大学理学部助手、助教を経て、2008年4月に東京学芸大学教育学部へ講師として着任し、2016年1月より現職。2009年度日本数学会賞建部賢弘賞奨励賞受賞。専門は位相幾何学（低次元トポロジー）で、主に「結び目理論」に関する研究をしている。

取材・編集／森本綺莉　田村怜士
イラスト／津波古薫